Not Dead… Yet!

An Introduction to Survival Analysis

Isaac Quintanilla Salinas

Access Presentation

https://www.inqs.info/pres/long_beach/pres_4_22.html

Email: isaac.qs@csuci.edu

Background Information

  • Background Information

  • Scenarios

  • Censoring

  • Survival Rate

  • Example

Survival Analysis

Survival Analysis is a set of tools to analyze time-to-event data. This leads to the survival rate which models the time to percentage of data to observe the event.

  • To determine the time until a percentile of the data achieves an event
  • Determine which factors may affect the survival rate

Scenarios

  • Background Information

  • Scenarios

  • Censoring

  • Survival Rate

  • Example

Colon Study

  • Colon cancer is a type of cancer found in the large intestine
  • Several risk factors affect the survival rate
  • We will look at how different medications affect the survival rate

Channel Island Birds

Channel Island Birds

  • We are interested in how long do bird eggs hatch since being laid

  • Determine the hatch rate for each species

  • What happens when there is missing data?

How do we determine the survival rate?

  • Measure from first recording to event of interest

  • Construct a probability of surviving up to a certain time point

Data Type

  • Data is typically recorded as time-to-event data

  • For biomedical studies, researchers are interested in time from diagnosis to death, known as time-to-death

Censoring

  • Background Information

  • Scenarios

  • Censoring

  • Survival Rate

  • Example

Censoring

  • Censoring is a mechanism where we do not observe the true time-to-event

  • Not all the time is observed

  • Three common types of censoring mechanisms: Right, Left, and Interval

CI Birds Example

You design a study where you want to record the time it takes for an egg to hatch for different species of birds.

You spend a week monitoring different bird nests and record times when eggs are laid.

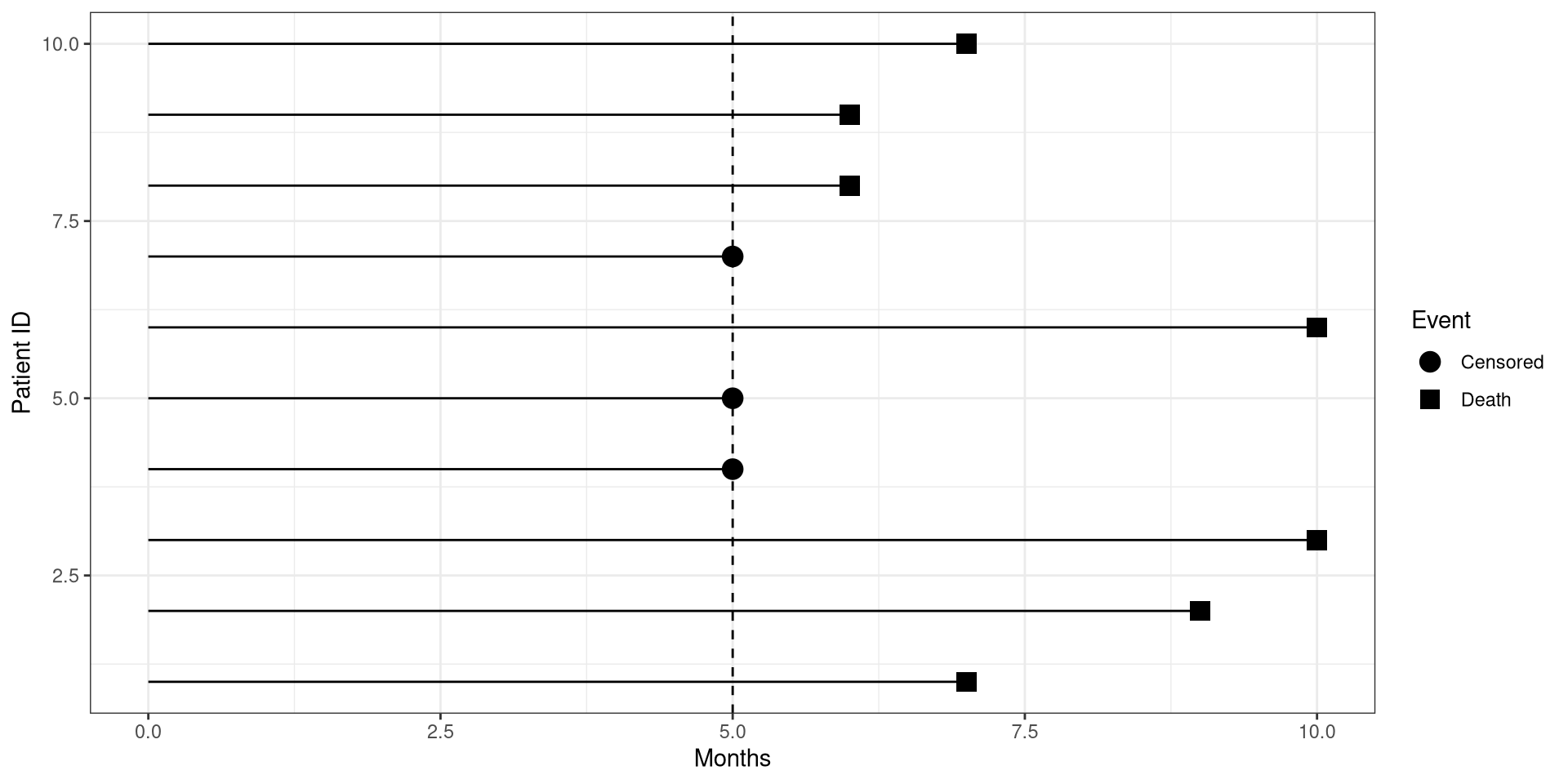
CI Birds Left Censoring

The day before the eggs hatched, your boat broke down and were not able to go to the islands for a week due to repairs.

During this time, 5 eggs hatched!

Left Censoring

library(ggplot2)
dat <- data.frame(ID = 1:10, 
                  t1 = c(7, 9, 10, 5, 5, 10, 5, 6, 6, 7) , 
                  censored = c(1, 1, 1, 0, 0, 1, 0, 1, 1, 1))
ggplot(dat, aes(x = ID, y = t1, shape = ifelse(censored, "Death", "Censored"))) + geom_point(size = 4) + 
    geom_linerange(aes(ymin = 0, ymax = t1)) +
    geom_hline(yintercept = 5, lty = 2) +
    coord_flip() + 
    scale_shape_manual(name = "Event", values = c(19, 15)) +
    # ggtitle("Left Censoring") + 
    xlab("Patient ID") +  ylab("Months") + 
    theme_bw()

CI Birds Interval Censoring

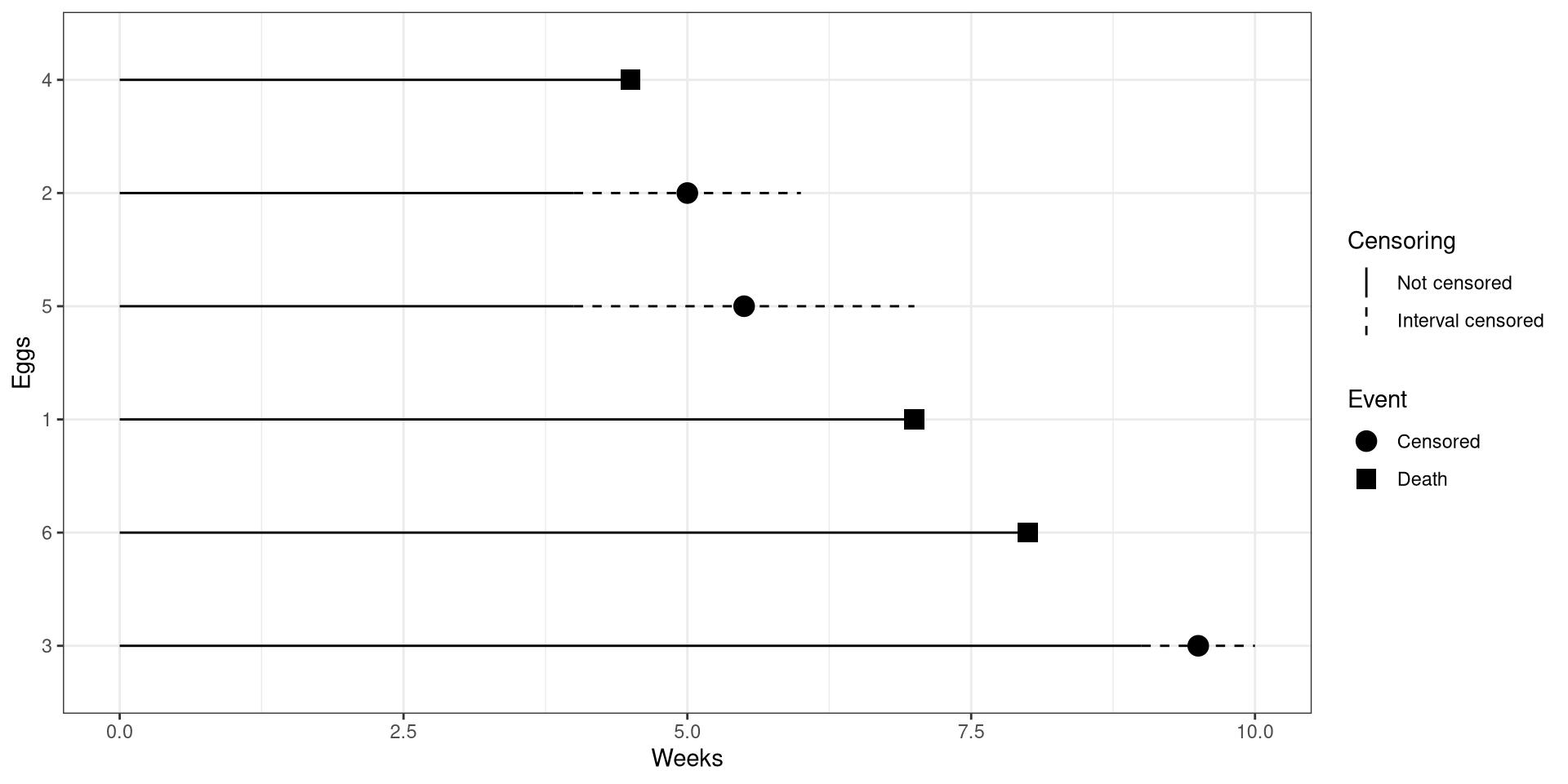
As you been going out to the islands each day to record whether eggs have hatched or not, you can’t travel to the islands for the next few days due to stormy weather.

During this time, 8 eggs hatched!

Interval Censoring

library(ggplot2)
dat <- structure(list(ID = 1:6, 
                      eventA = c(0L, 1L, 1L, 0L, 1L, 0L),
                      eventB = c(1L, 0L, 0L, 1L, 0L, 1L), 
                      t1 = c(7, 4, 9, 4.5, 4, 8), 
                      t2 = c(7, 6, 10, 4.5, 7, 8),
                      censored = c(0, 1, 1, 0, 1, 0)), 
                 .Names = c("ID", "eventA", "eventB", "t1", "t2", "censored"), 
                 class = "data.frame", row.names = c(NA, -6L))

dat$event <- with(dat, ifelse(eventA, "Censored", "Death"))

dat$id.ordered <- factor(x = dat$ID, levels = order(dat$t2, decreasing = T))

ggplot(dat, aes(x = id.ordered)) + 
    geom_linerange(aes(ymin = 0, ymax = t1)) + 
    geom_linerange(aes(ymin = t1, ymax = t2, 
                       linetype = as.factor(censored))) +  
    geom_point(aes(y = ifelse(censored, 
                              t1 + (t2 - t1) / 2, t2), 
                   shape = event), size = 4) +
    coord_flip() + 
    scale_linetype_manual(name = "Censoring", values = c(1, 2), 
        labels = c("Not censored", "Interval censored")) +
    scale_shape_manual(name = "Event", values = c(19, 15)) +
    # ggtitle("Interval Censoring") + 
    xlab("Eggs") +  ylab("Weeks") + 
    theme_bw()

CI Birds Right Censoring

It is the end of the study, and their are 5 more eggs that have not hatched yet!

Additionally, a colleague has informed you that some eggs were eaten by reptiles through out the study. They obtained the day they were eaten or lost.

Right Censoring

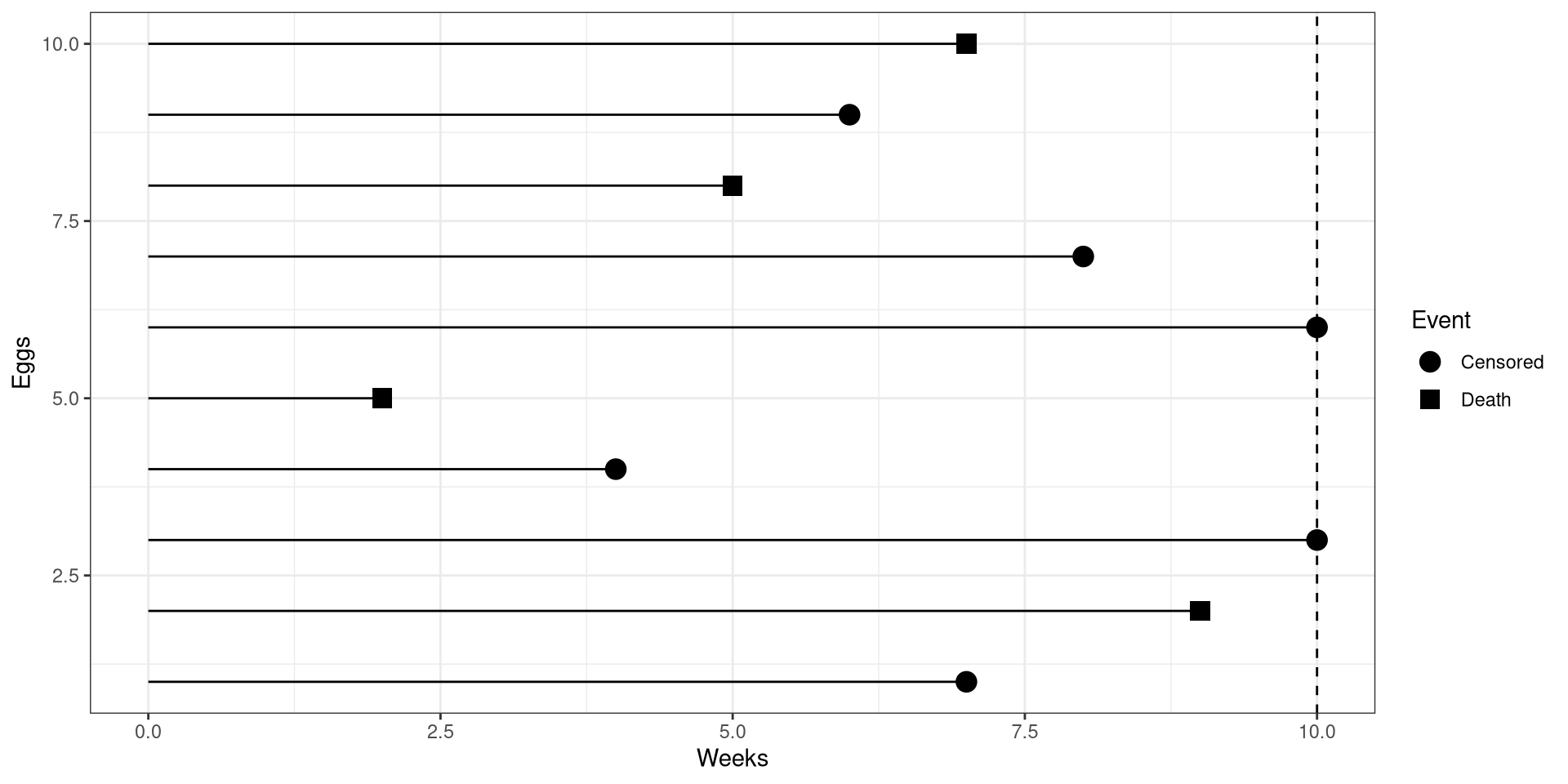
library(ggplot2)
dat <- data.frame(ID = 1:10, 
                  t1 = c(7, 9, 10, 4, 2, 10, 8, 5, 6, 7) , 
                  censored = c(0, 1, 0, 0, 1, 0, 0, 1, 0, 1))
ggplot(dat, aes(x = ID, y = t1, 
                shape = ifelse(censored, "Death", "Censored"))) +
    geom_point(size = 4) + 
    geom_linerange(aes(ymin = 0, ymax = t1)) +
    geom_hline(yintercept = 10, lty = 2) +
    coord_flip() + 
    scale_shape_manual(name = "Event", values = c(19, 15)) +
    # ggtitle("Right Censoring") + 
    xlab("Patient ID") +  ylab("Months") + 
    theme_bw()

Censoring

  • Censoring affects the time-to-event information

  • However, we obtain some information when data is censored

  • Incorporate methods to utilize partial information

  • Censoring is independent of time-to-event generation

Survival Rate

  • Background Information

  • Scenarios

  • Censoring

  • Survival Rate

  • Example

Survival Curve

  • The survival curve will determine what is the probability of surviving up to a certain time

  • A survival curve accounts for both censored and uncensored data

  • A survival curve can be used to determine the median survival time of a disease

    • Or the time for at least half of the eggs to hatch

Data Notation

Let \(\{t_j,d_j,R_j\}^D_{j=1}\) denote the survival data, where \(t_1<t_2<\cdots<t_D\) are the ordered distinct observed event times, \(d_j\) represents the number of events at time point \(t_j\), and \(R_j\) denotes the number of subjects still at risk of experiencing the event at \(t_j\).

Kaplan-Meier Estimator

\[ \hat{S}(t) =\left\{\begin{array}{cc} 1 & t=0 \\ \prod_{i:t_j \le t} \left( 1 - \frac{d_j}{R_j} \right) & t_j < t \end{array}\right. \]

Standard Error

\[ \widehat{SE}\{\hat S(t)\}=\sqrt{\hat S^2(t)\sum_{t_j\leq t}\frac{d_j}{R_j(R_j-d_j)}}. \]

Survival Curve

library(survival)
library(ggsurvfit)
library(magrittr)
aml %$% survfit(Surv(time, status) ~ 1)  %>% 
      ggsurvfit(linewidth = 1) +
      add_quantile(y_value = 0.5, color = "gray50", linewidth = 0.75)

Example

  • Background Information

  • Scenarios

  • Censoring

  • Survival Rate

  • Example

Data

We will be looking at the df_colon data set from the ggsurvfit R package.

library(tidyverse)
library(ggsurvfit)
library(DT)
adj_df <- df_colon %>% select(id, rx, time, status)
datatable(adj_df, options = list(pageLength = 5, dom = 'i'))

Fitting Curve

The survival package contains the necessary functions to fit a model:

  • Surv: Creates an outcome variable
  • survfit: Fits the survival function
1library(survival)
2outcome <- Surv(data$time, data$censor)
3model <- survfit(outcome ~ 1)
1
Loads the survival package
2
Create survival outcome object
3
Fits Survival Model

Plotting the Survival Function

The ggsurvfit package provides a set of tools to plot the survival function in a ggplot format. The primary functions are:

  • ggsurvfit: Plots Survival Function

  • add_quantile: Adds line on the percentile

  • add_confidence_interval: Adds pointwise error bars to the plot.

ggsurvfit(model) + 
  add_quantile(y_value = 0.5) +
  add_confidence_interval()

Fitting Curve By Groups

If we are interested in fitting survival curves by groups, we can specify the variable that we want to adjust by.

survfit(Surv(time, censor) ~ group, data)

Once the model is fitted, feed it to ggsurvfit and the function will do the rest.

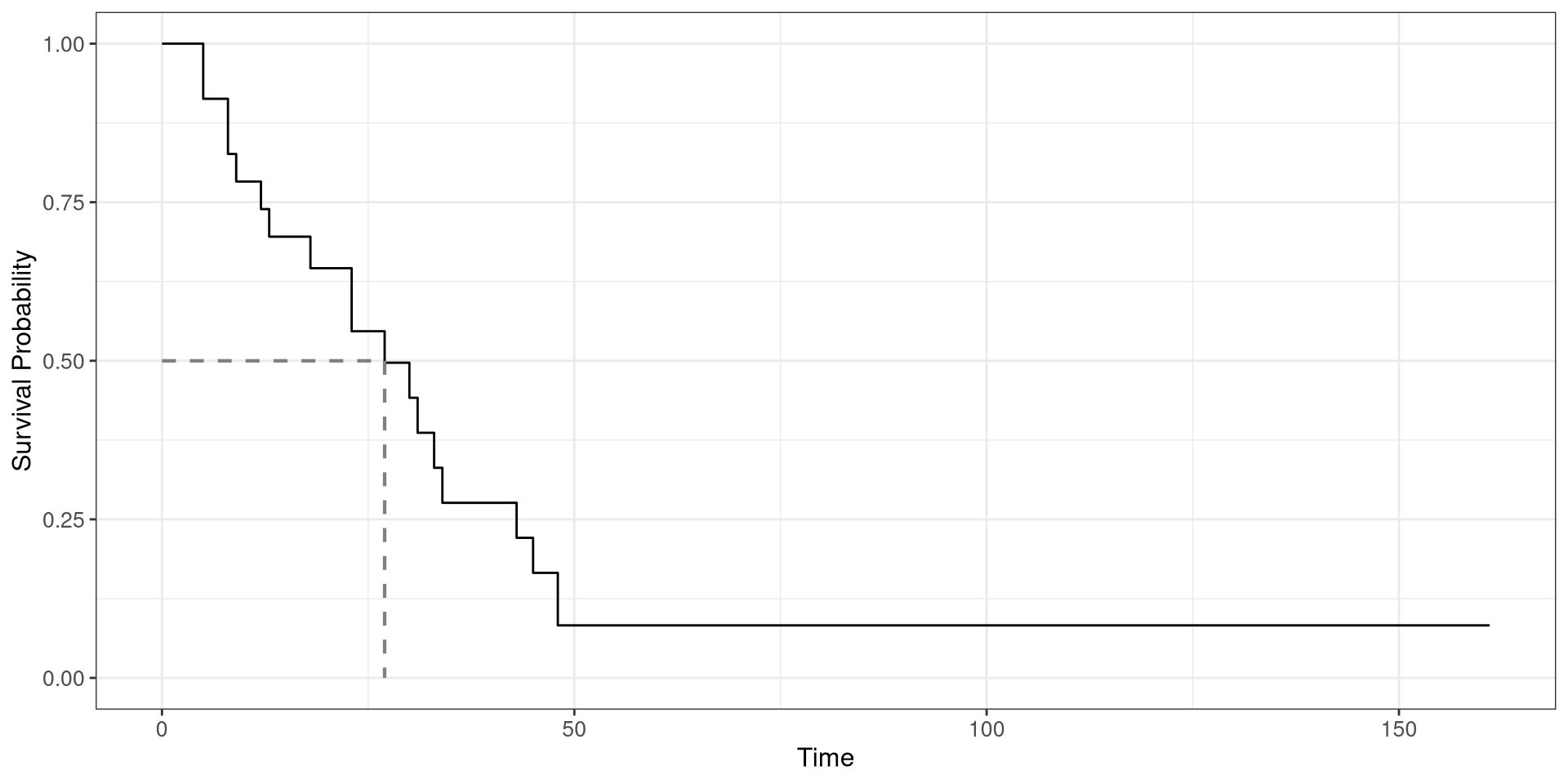
Colon Survival Curve

  • Fit a survival curve using df_colon from the ggsurvfit package.
  • time: time-to-death
  • status: censoring status
  • Plot the survival curve and add a line indicating the 50th percentile

library(survival)
library(ggsurvfit)
library(magrittr)
library(tidyverse)
df_colon %$% survfit(Surv(time, status) ~ 1)  %>% 
      ggsurvfit() +
      add_quantile(y_value = 0.5, color = "gray50", linewidth = 0.75)

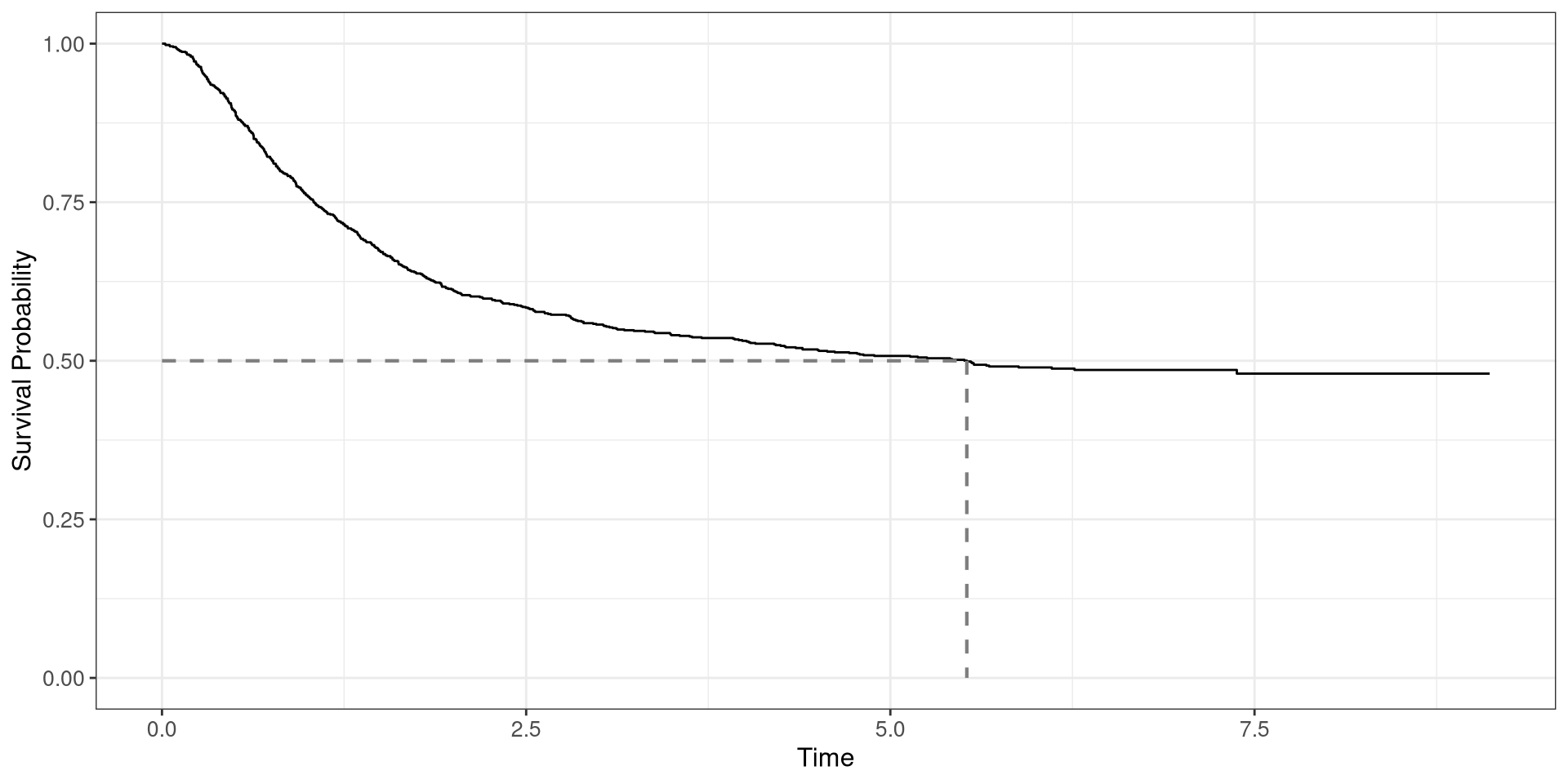
Colon Survival Curve

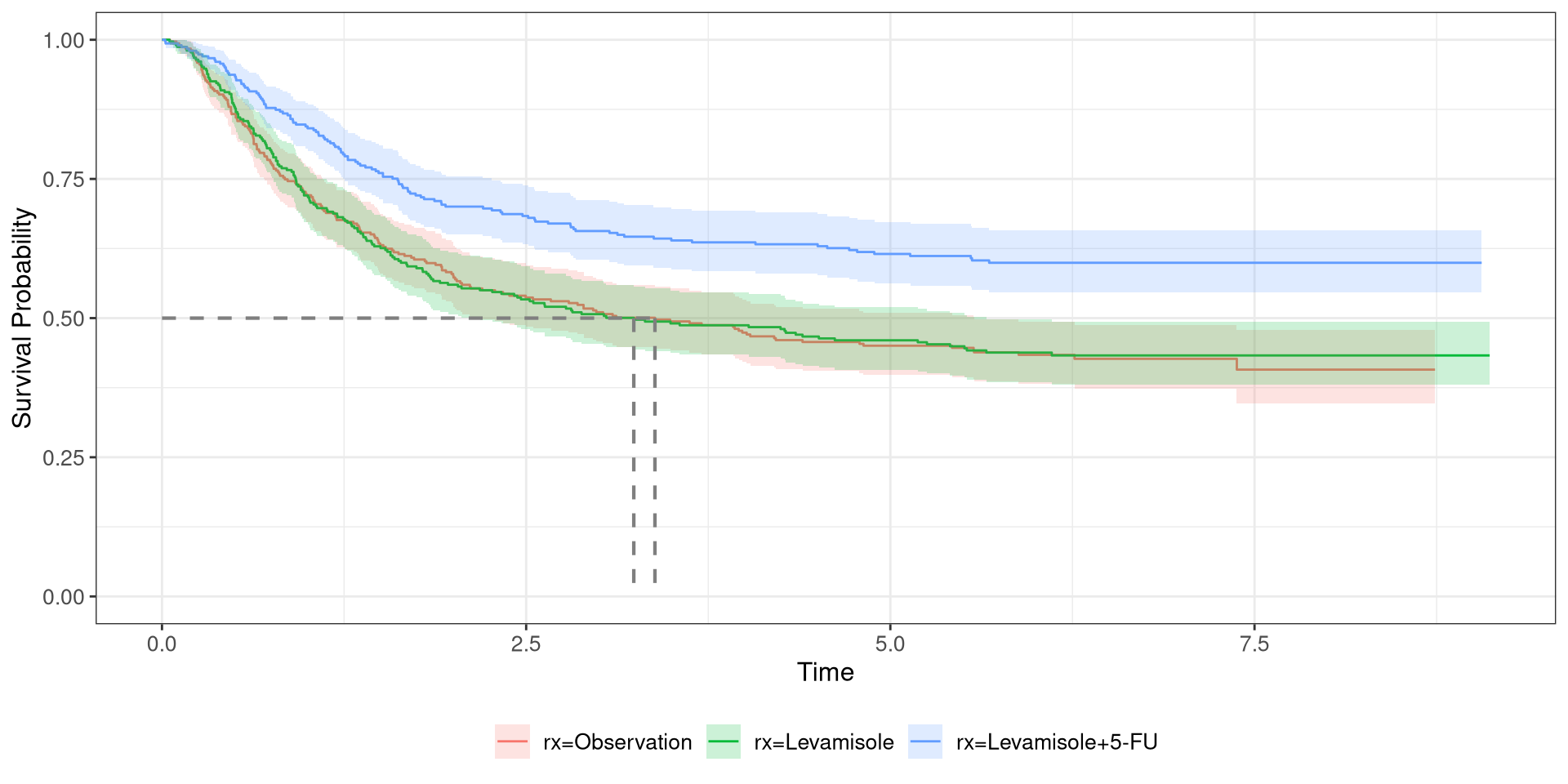
  • Fit a survival curve using df_colon, stratified by treatment regimen
  • time: time-to-death
  • status: censoring status
  • rx: treatment regimen
  • Plot the curvival curve and add a line indicating the 50th percentile

df_colon %$% survfit(Surv(time, status) ~ rx)  %>% 
      ggsurvfit() +
      add_quantile(y_value = 0.5, color = "gray50", linewidth = 0.75)

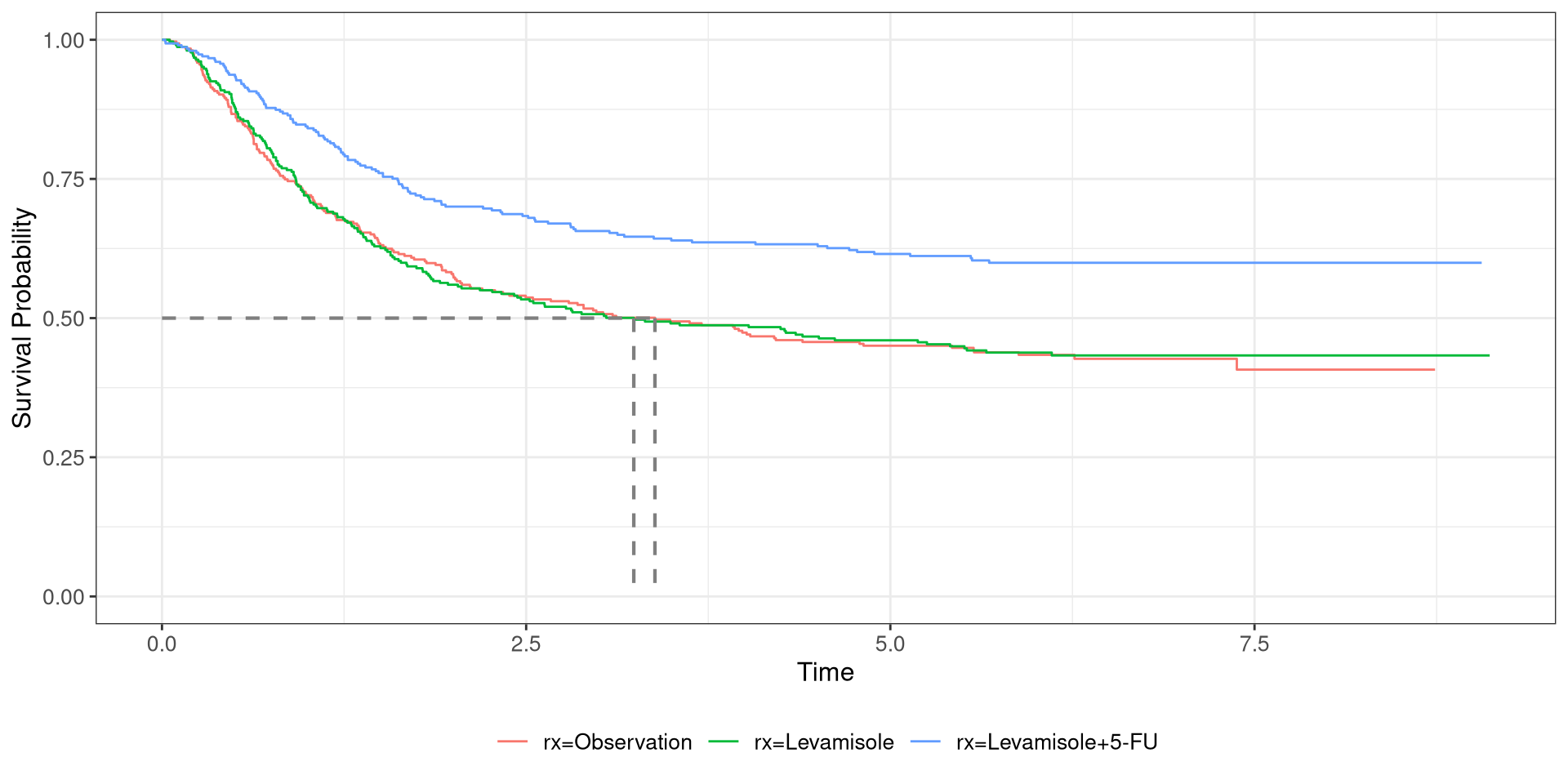
Hypothesis Testing

  • When stratifying the data, Levamisole+5 FU performed better than the other regimens
  • Is this a significant improvement? Or due to random chance?
  • Add Confidence Intervals to see if there is a difference

Colon Survival Curve

Add confidence intervals to the previous plot.

df_colon %$% survfit(Surv(time, status) ~ rx)  %>% 
      ggsurvfit() +
      add_confidence_interval() +
      add_quantile(y_value = 0.5, color = "gray50", linewidth = 0.75)